8.2. Analyse numérique

8.2.1. Résolution d’équations par dichotomie

Il s’agit ici de calculer une valeur approchée d’une solution d’une équation du type \(f(x)=0\). On ne cherche pas à obtenir une expression exacte d’une telle solution, ce qui est de toute façon évidemment impossible de manière générale.

On suppose qu’on dispose d’une fonction \(f\) continue et strictement monotone sur un intervalle \([a,b]\) vérifiant \(f(a)f(b)\leq0\). Le théorème des valeurs intermédiaires garantit l’existence d’une unique solution à l’équation \(f(x)=0\) sur l’intervalle \([a,b]\). Pour obtenir une valeur approchée de cette solution, on procède par dichotomie :

1. On calcule \(c=(a+b)/2\) et \(f(c)\).

2. Si \(f(a)f(c)\leq0\), la solution appartient à l’intervalle \([a,c]\). Sinon, elle appartient à l’intervalle \([c,b]\).

3. Dans le premier cas, on remplace \(b\) par \(c\) tandis que dans le second cas, on remplace \(a\) par \(c\).

4. On répète les étapes 1., 2. et 3. tant que la longeur de l’intervalle \([a,b]\) est supérieur à une précision \(\epsilon\) donnée.

5. La valeur de \(c\) est alors une valeur appochée de la solution de \(f(x)=0\) à \(\epsilon/2\) près.

In [1]: def dicho(f, a, b, eps):
   ...:     while abs(b-a) > eps:
   ...:         c = (a + b) / 2
   ...:         if f(a) * f(c) <= 0:
   ...:             b = c
   ...:         else:
   ...:             a = c
   ...:     return (a+b) / 2
   ...: 

In [2]: from math import sin

In [3]: dicho(sin, 2, 4, .0001)
Out[3]: 3.141571044921875

Il est à remarquer que le module scipy dispose déjà de fonctions pouvant résoudre de manière approchée des équations du type \(f(x)=0\).

In [4]: from scipy.optimize import fsolve

In [5]: from math import cos

In [6]: f = lambda x: cos(x**2)

In [7]: x0 = fsolve(f, 0)

In [8]: x0
Out[8]: array([-49.99136881])

In [9]: f(*x0)
Out[9]: -1.063024370691732e-13

8.2.2. Calcul d’intégrales

On expose ici des algorithmes de calcul approché d’intégrales [1]. A nouveau, on ne cherche pas à obtenir des expressions exactes de ces intégrales.

8.2.2.1. Méthode des rectangles

On peut approcher une intégrale par une somme d’aire de rectangles comme l’indique la figure suivante.

Plus précisément, en posant \(x_k=a+k(b-a)/n\) où \(n\) désigne le nombre de rectangles :

\[\begin{split}\begin{align*} R_n&=\frac{b-a}{n}\sum_{k=0}^{n-1}f(x_k)\approx\int_a^bf(t)\,\mathrm{dt}&\text{(rectangles verts)}\\ S_n&=\frac{b-a}{n}\sum_{k=1}^nf(x_k)\approx\int_a^bf(t)\,\mathrm{dt}&\text{(rectangles rouges)} \end{align*}\end{split}\]

On peut alors proposer la fonction suivante pour approcher l’intégrale d’une fonction \(f\) sur un intervalle \([a,b]\).

In [10]: def rectangles(f, a, b, N, side):
   ....:     pas = (b-a) / N
   ....:     x = a
   ....:     somme = 0
   ....:     for _ in range(N):
   ....:         if side:
   ....:             somme += f(x)
   ....:         x += pas
   ....:         if not side:
   ....:             somme += f(x)
   ....:     return somme / N
   ....: 

In [11]: rectangles(lambda x: x**2, 0, 1, 100, True)
Out[11]: 0.3283500000000004

In [12]: rectangles(lambda x: x**2, 0, 1, 100, False)
Out[12]: 0.33835000000000043

Les sommes \(R_n\) et \(S_n\) sont appelées des sommes de Riemann et on peut même prouver que pour une fonction \(f\) continue,

\[\lim_{n\to+\infty}S_n=\lim_{n\to+\infty}T_n=\int_a^bf(t)\,\mathrm{dt}\]

En particulier, l’appoximation de l’intégrale \(\int_a^bf(t)\,\mathrm{dt}\) est d’autant meilleure que le nombre \(n\) de rectangles est grand, ce qui se conçoit très bien géométriquement [2].

8.2.2.2. Méthode des trapèzes

On peut également apporcher une intégrale comme une somme d’aires de trapèzes comme sur la figure suivante. Bien évidemment, l’approximation de l’intégrale est meilleure qu’avec des rectangles.

A nouveau, en posant \(x_k=a+k(b-a)/n\) où \(n\) désigne le nombre de trapèzes :

\[\begin{split}T_n=\frac{b-a}{n}\sum_{k=0}^{n-1}\frac{f(x_k)+f(x_{k+1})}{2}\approx\int_a^bf(t)\,\mathrm{dt}\\\end{split}\]

On peut évidemment remarquer que \(T_n=(R_n+S_n)/2\). En fait, la somme précédente peut se réécrire de manière différente :

\[T_n=\frac{b-a}{n}\left(\frac{f(a)+f(b)}{2}+\sum_{k=1}^{n-1}f(x_k)\right)\]

Cette nouvelle formule permet de calculer \(T_n\) en effectuant moins d’opérations qu’avec la formule précédente. On peut alors donner l’algorithme suivant.

In [13]: def trapezes(f, a, b, N):
   ....:     pas = (b-a) / N
   ....:     x = a
   ....:     somme = (f(a) + f(b)) / 2
   ....:     for _ in range(N-1):
   ....:         x += pas
   ....:         somme += f(x)
   ....:     return somme / N
   ....: 

In [14]: trapezes(lambda x: x**2, 0, 1, 100)
Out[14]: 0.3333500000000004

À faire

Méthodes de quadrature

8.2.3. Résolution d’équations différentielles

L’objectif est de résoudre numériquement des équations différentielles : c’est-à-dire qu’on ne cherche pas des expressions explicites des solutions mais des valeurs approchées [3].

Pour commencer, on traitera le cas de problème de Cauchy d’ordre 1.

\[\begin{split}\left\{ \begin{aligned} y'&=f(t,y)\\ y(t_0)&=y_0 \end{aligned} \right.\end{split}\]

On rappelle qu’un tel problème consiste en la donnée d’une équation différentielle résolue d’ordre 1 \(y'=f(t,y)\) et d’une condition initiale \(y(t_0)=y_0\). Le théorème de Cauchy-Lipschitz garantit l’existence et l’unicité d’une solution à ce problème lorsque \(f\) est suffisamment règulière.

L’idée est d’utiliser une approximation affine de la fonction solution : \(y(t+\Delta\!t)\approx y(t)+y'(t)\Delta\!t\). Le calcul de \(y'(t)\) est possible grâce à l’équation différentielle si l’on connaît \(y(t)\) puisque \(y'(t)=f(t,y(t))\). On itère ce processus pour calculer des valeurs approchées à des intervalles de temps réguliers. Plus précisément, en posant \(t_k=t_0+k\Delta\!t\), on a alors

\[\begin{split}\begin{alignat}{2} y(t_1) & \approx y(t_0)+y'(t_0)\Delta\!t & = y(t_0)+f(t_0,y_0)\Delta\!t &= y_1\\ y(t_2) & \approx y(t_1)+y'(t_1)\Delta\!t & \approx y(t_1)+f(t_1,y_1)\Delta\!t &= y_2\\ y(t_3) & \approx y(t_2)+y'(t_2)\Delta\!t & \approx y(t_2)+f(t_2,y_2)\Delta\!t &= y_3\\ \dots \end{alignat}\end{split}\]

La méthode que l’on vient de décrire porte le nom de méthode d’Euler.

def euler(f, t0, y0, pas, nb):
    t = t0
    y = y0
    liste_t = [t]
    liste_y = [y]
    for _ in range(nb):
        y += f(t, y) * pas
        t += pas
        liste_t.append(t)
        liste_y.append(y)
    return liste_t, liste_y

Par exemple, on calcule ici une solution approchée du système de Cauchy

\[\begin{split}\left\{ \begin{aligned} y'&=\cos(t)y\\ y(0)&=1 \end{aligned} \right.\end{split}\]

from math import cos
f = lambda t, y: cos(t) * y
liste_t, liste_y = euler(f, 0, 1, .01, 1000)

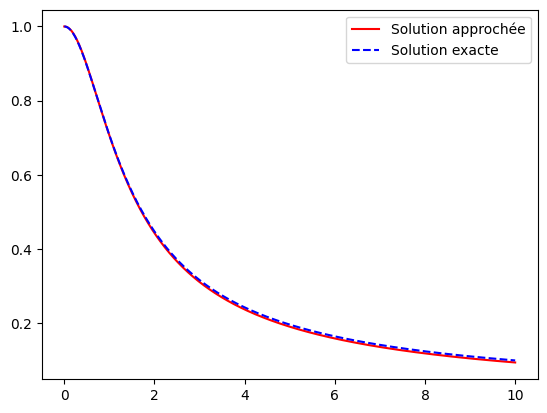
On peut tracer la courbe de la solution approchée que l’on peut comparer à la courbe de la solution exacte. En effet, on montre sans peine que l’unique solution de ce problème de Cauchy est la fonction \(x\mapsto e^{\sin(x)}\).

import matplotlib.pyplot as plt
import numpy as np

# Tracé de la solution approchée
plt.plot(liste_t, liste_y, color='red', label='Solution approchée');

# Tracé de la solution exacte
x = np.linspace(0, 10, 1000)
y = np.exp(np.sin(x))
plt.plot(x, y, '--', color='blue', label='Solution exacte');

plt.legend();

Bien entendu, l’approximation affine \(y'(t+\Delta\!t)\approx f(t)+f'(t)\Delta\!t\) est d’autant meilleure que \(\Delta\!t\) est petit.

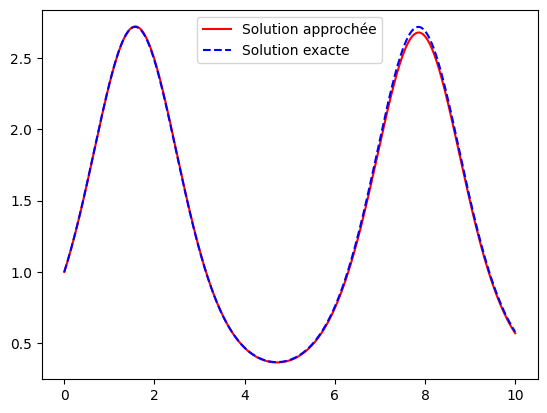
On peut adapter la méthode au cas d’un système différentiel d’ordre 1. Soit par exemple à résoudre le système différentiel suivant.

\[\begin{split}\left\{ \begin{aligned} x'&=\cos(t)x+\sin(t)y\\ y'&=\sin(t)x+\cos(t)y\\ (x(0),y(0))&=(1,0) \end{aligned} \right.\end{split}\]

def euler(f, t0, X0, pas, nb):
    t = t0
    X = X0
    liste_t = [t]
    liste_X = [X]
    for _ in range(nb):
        X = [x + u * pas for x, u in zip(X, f(t, X))]
        t += pas
        liste_t.append(t)
        liste_X.append(X)
    return liste_t, liste_X

from math import cos, sin
f = lambda t, X: [cos(t) * X[0] + sin(t) * X[1], sin(t) * X[0] + cos(t) * X[1]]
liste_t, liste_X = euler(f, 0, [1, 0], .01, 1000)

import matplotlib.pyplot as plt
import numpy as np

plt.figure();

# Tracé de la solution approchée
plt.plot(*zip(*liste_X), color='red', label='Solution approchée');

# Tracé de la solution exacte
t = np.linspace(0, 10, 1000)
x = np.exp(np.sin(t)) * np.cosh(1 - np.cos(t))
y = np.exp(np.sin(t)) * np.sinh(1 - np.cos(t))
plt.plot(x, y, '--', color='blue', label='Solution exacte');

plt.legend();

On sait qu’il est toujours possible de ramener une équation différentielle scalaire d’ordre strictement supérieur à 1 à un système différentiel d’ordre 1.

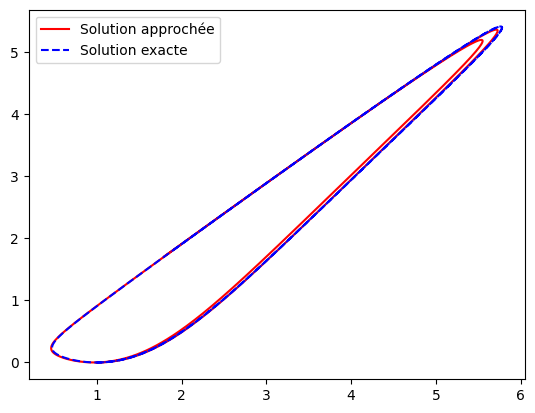
Par exemple, si l’on désire résoudre le problème de Cauchy

\[\begin{split}\left\{\begin{aligned} y''+\frac{2t}{1+t^2}y'+\frac{1}{(1+t^2)^2}y&=0\\ (y(0),y'(0))&=(1,0) \end{aligned}\right.\end{split}\]

on peut se ramener au système différentiel d’ordre 1 suivant

\[\begin{split}\left\{\begin{aligned} y'&=z\\ z'&=-\frac{2t}{1+t^2}z-\frac{1}{(1+t^2)^2}y\\ (y(0),z(0))&=(1,0) \end{aligned}\right.\end{split}\]

f = lambda t, X: [X[1], -X[0] / (1 + t**2)**2 - 2 * t / (1 + t**2) *X[1]]
liste_t, liste_X = euler(f, 0, [1, 0], .01, 1000)

import matplotlib.pyplot as plt
import numpy as np

# Tracé de la solution approchée
plt.plot(liste_t, [X[0] for X in liste_X], color='red', label='Solution approchée');

# Tracé de la solution exacte
t = np.linspace(0, 10, 1000)
y = 1/np.sqrt(1 + t**2)
plt.plot(t, y, '--', color='blue', label='Solution exacte');

plt.legend();

[1]

Le module scipy.integrate dispose déjà d’une fonction quad à cet effet.

À faire

Renvoyer vers le chapitre scipy/numpy

In [15]: from scipy.integrate import quad

In [16]: quad(lambda x: 1 / x**2, 1, 2)
Out[16]: (0.49999999999999994, 5.551115123125782e-15)

La fonction quad renvoie un couple formé de l’approximation de l’intégrale et d’une majoration de l’erreur d’approximation.

[2]

Il ne faut cependant pas crier victoire trop tôt. Tout d’abord, le temps de calcul augmente avec \(n\). De plus, chaque opération dans l’algorithme entraîne une erreur d’arrondi minime mais, le nombre d’opérations augmentant avec \(n\), le cumul de ces erreurs d’arrondi finit par dépasser le gain en précision lorsque \(n\) est très grand.

[3]

Le module scipy.integrate dispose déjà d’une fonction odeint à cet effet.

À faire

Renvoyer vers le chapitre scipy/numpy