On sait que les images des racines $n^\text{èmes}$ de l’unité forment un polygone régulier. On expose dans ce post la construction du pentagone régulier.
Calcul de $\cos\frac{2\pi}{5}$
Il suffit de faire un tour par les complexes. En posant $\omega=e^\frac{2i\pi}{5}$, on a clairement $1+\omega+\omega^2+\omega^3+\omega^4=\frac{\omega^5-1}{\omega-1}=0$. Or $\omega+\omega^4=\omega+\frac{1}{\omega}=2\cos\frac{2\pi}{5}$ et $\omega^2+\omega^3=\omega^2+\frac{1}{\omega^2}=2\cos\frac{4\pi}{5}=2(2\cos^2\frac{2\pi}{5}-1)$. Il s’ensuit que $\cos\frac{2\pi}{5}$ est racine du polynôme $4X^2+2X-1$. Puisque $\cos\frac{2\pi}{5}$ est positif, $\cos\frac{2\pi}{5}=\frac{\sqrt5-1}{4}$.
Construction d’un repère orthonormé et du cercle trigonométrique.
On se donne deux points $A$ et $B$ du plan et l’on convient que $AB=1$. On peut alors tracer le cercle $\mathscr{C}$ de centre $A$ passant par $B$. On note $C$ le point d’intersection du cercle $\mathscr{C}$ et de la droite $(AB)$. On peut tracer la médiatrice du segment $[AC]$ à l’aide d’un compas1. On note $D$ et $E$ les points d’intersection du cercle $\mathscr{C}$ et de cette médiatrice.
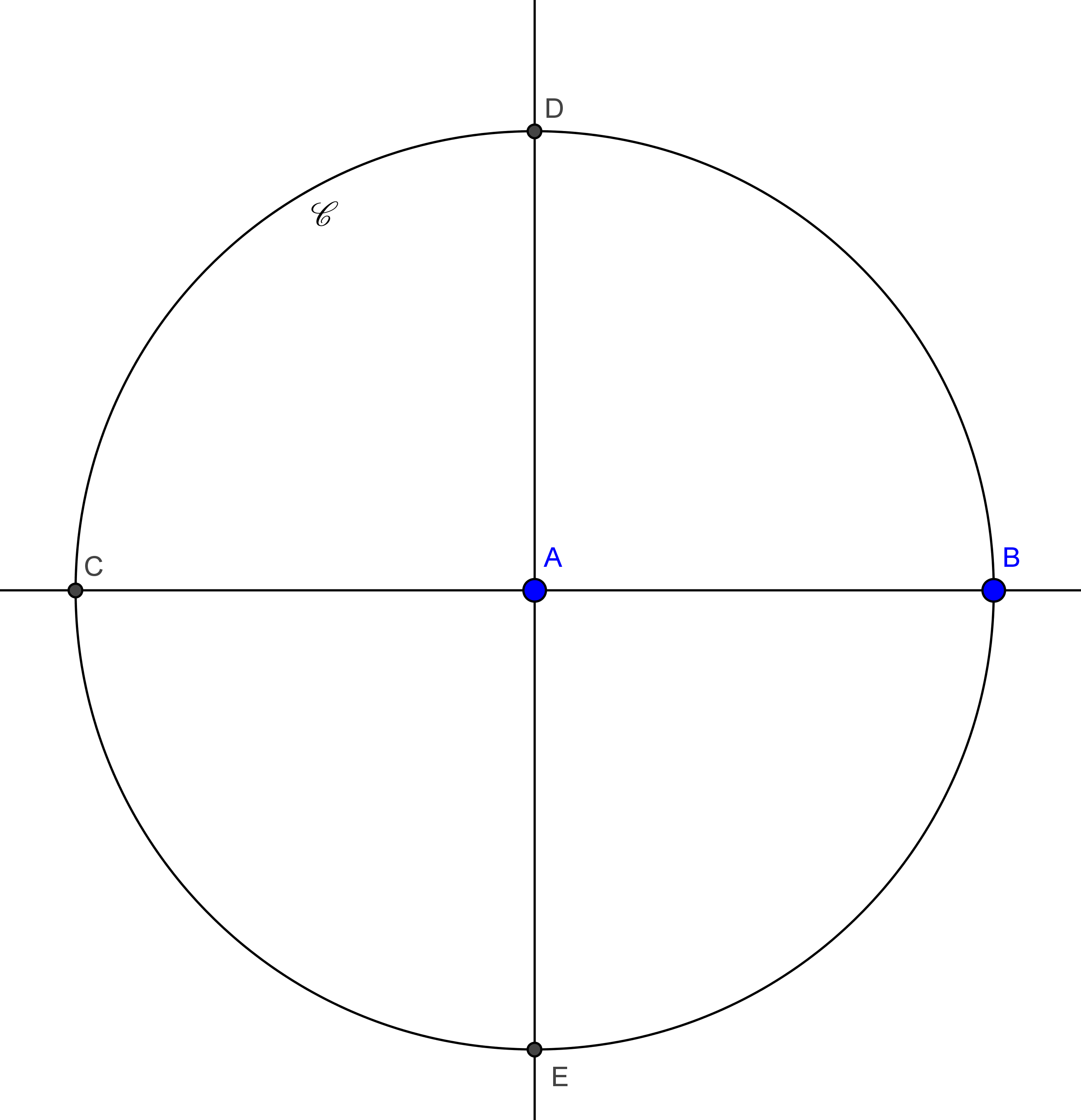
Construction de $\cos\frac{2\pi}{5}$
Dans un premier temps, on construit le milieu $F$ du segment $[AC]$. On trace alors le cercle $\Gamma$ de centre $F$ passant par $D$. Le théorème de Pythagore permet d’affirmer que $FD=\frac{\sqrt5}{2}$. Notons $G$ le point d’intersection du cercle $\Gamma$ et du segment $[AB]$. Il est évident que que $AG=\frac{\sqrt5-1}{2}$. On trace alors la médiatrice du segment $[AG]$ qui coupe le segment $[AB]$ en un point $H$ ainsi que le cercle $\mathscr{C}$ en des points $I$ et $J$. On a alors bien $AH=\frac{\sqrt5-1}{4}=\cos\frac{2\pi}{5}$.
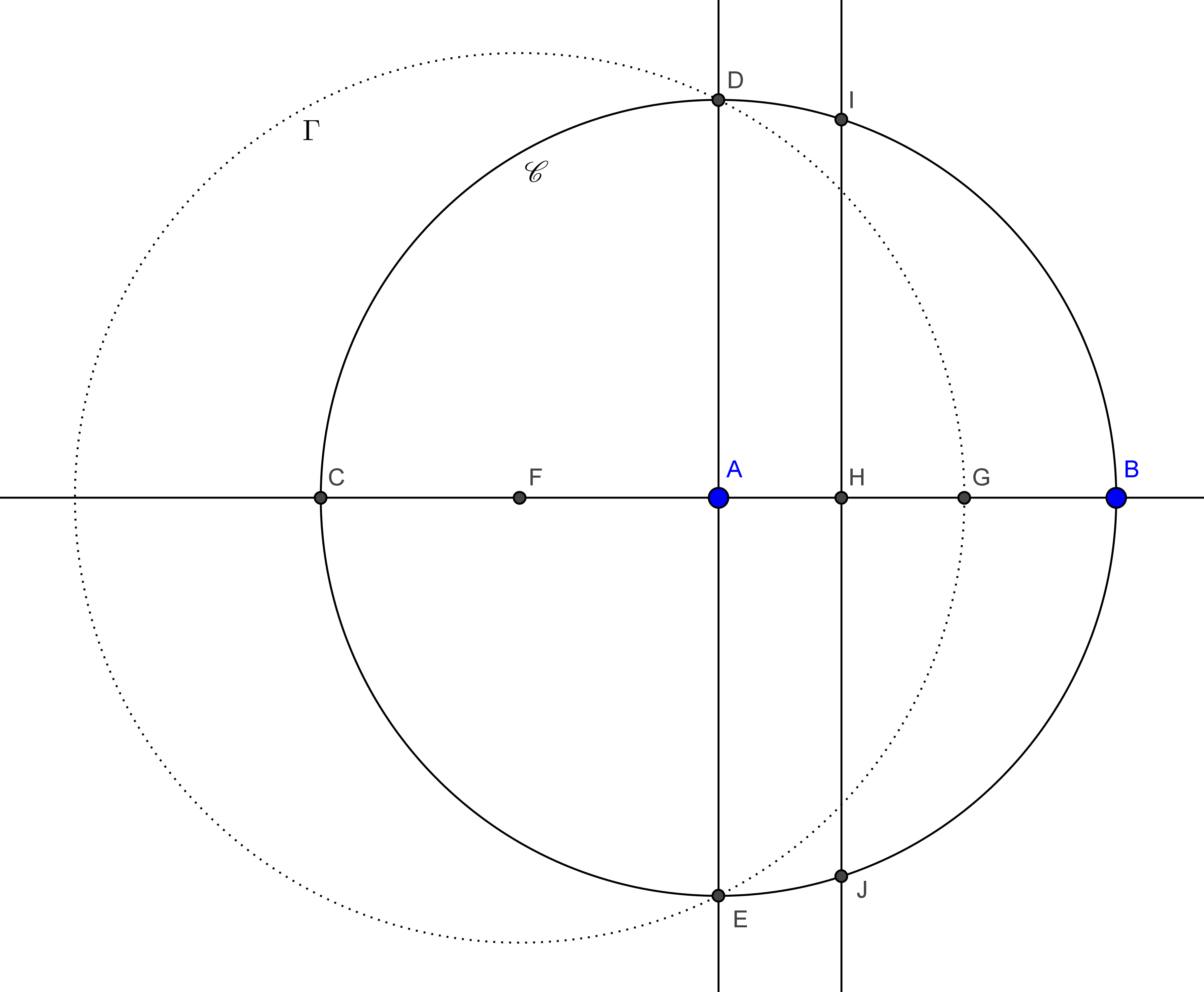
Construction du pentagone régulier
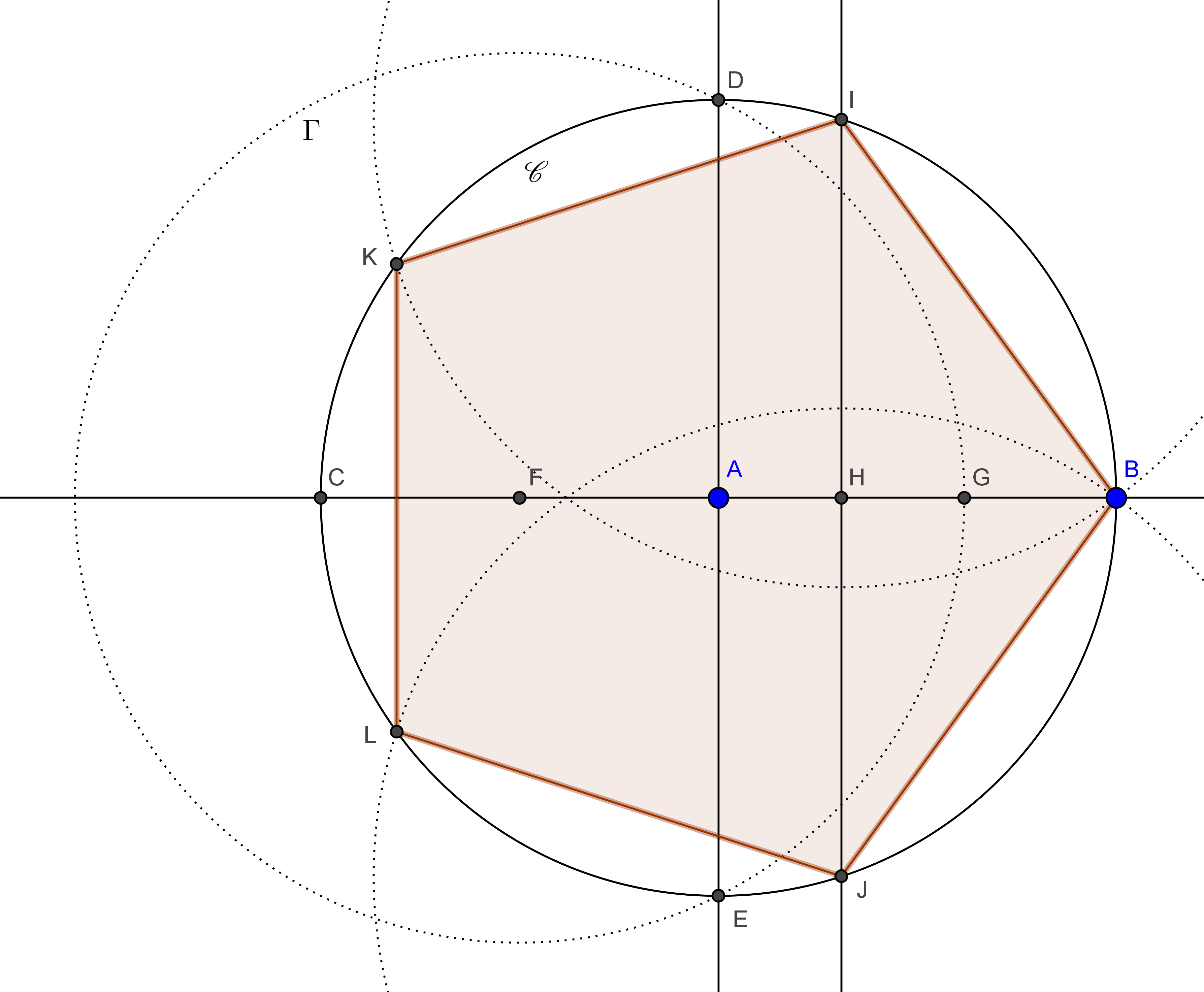
Puisque le cercle $\mathscr{C}$ a pour rayon 1, les angles $\widehat{BAI}$ et $\widehat{BAJ}$ ont pour mesure $\frac{2\pi}{5}$. Il ne reste alors plus qu’à tracer les cercles de centre $I$ et $J$ passant par $B$ : ceux-ci coupent le cercle $\mathscr{C}$ en des points $K$ et $L$. Le pentagone $BIKLJ$ est alors régulier.
Pour aller plus loin
On peut se demander s’il existe des procédés de construction à la règle et au compas d’autres polygones réguliers. Par exemple, une telle construction de l’heptadécagone2 régulier a été proposée par le prince des mathématiciens, Carl-Friedrich Gauß, à l’âge de 19 ans. Dans la foulée, ce dernier a prouvé que tout polygone dont le nombre de côtés est le produit d’une puissance de 2 et de nombres premiers de Fermat3 distincts est constructible à la règle et au compas. L’heptadécagone régulier est effectivement constructible à la règle et au compas puisque $17=2^{2^2}+1$ est un nombre premier de Fermat. La réciproque de ce résultat est également vraie et a été prouvée ultérieurement par Wantzel.