Toutes les fractions considérées dans cet article sont des fractions irréductibles d’entiers naturels. On adjoint à ces fractions la fraction $\frac{1}{0}$ dont on convient raisonnablement qu’elle est strictement supérieure à toutes les autres.

Médiante de deux fractions

On appelle médiante de deux fractions $\frac{a}{b}$ et $\frac{c}{d}$ la fraction $\frac{a}{b}\oplus\frac{c}{d}=\frac{a+c}{b+d}$.

Pour une fraction irréductible $r=\frac{p}{q}$, on pose $S(r)=p+q$.

Pour deux fractions d’entiers naturels $r_1=\frac{a}{b}$ et $r_2=\frac{c}{d}$, on pose $\Delta(r_1,r_2)=bc-ad$

Soient $r_1$ et $r_2$ deux fractions.
  • $\Delta(r_1,r_2)=-\Delta(r_2,r_1)$.
  • $r_1\lt r_2$ si et seulement si $\Delta(r_1,r_2)\gt0$ et $r_1=r_2$ si et seulement si $\Delta(r_1,r_2)=0$.
  • $\Delta(r_1,r_1\oplus r_2)=\Delta(r_1\oplus r_2,r_2)=\Delta(r_1,r_2)$.
  • Si $r_1\lt r_2$, alors $r_1\lt r_1\oplus r_2\lt r_2$.

Calcul de suites finies

On construit une suite de suites finies de rationnels par récurrence. On pose $u_0=\left(\frac{0}{1},\frac{1}{0}\right)$ et une fois une suite finie $u_n$ construite, on construit la suite $u_{n+1}$ en intercalant entre deux fractions consécutives de la suite $u_n$ la médiante de ces deux fractions1. On trouve donc successivement

\[\begin{align*} u_0&=\left(\frac{0}{1},\frac{1}{0}\right)\\ u_1&=\left(\frac{0}{1},\frac{1}{1},\frac{1}{0}\right)\\ u_2&=\left(\frac{0}{1},\frac{1}{2},\frac{1}{1},\frac{2}{1},\frac{1}{0}\right)\\ u_3&=\left(\frac{0}{1},\frac{1}{3},\frac{1}{2},\frac{2}{3},\frac{1}{1},\frac{3}{2},\frac{2}{1},\frac{3}{1},\frac{1}{0}\right)\\ u_4&=\left(\frac{0}{1},\frac{1}{4},\frac{1}{3},\frac{2}{5},\frac{1}{2},\frac{3}{5},\frac{2}{3},\frac{3}{4},\frac{1}{1},\frac{4}{3},\frac{3}{2},\frac{5}{3},\frac{2}{1},\frac{5}{2},\frac{3}{1},\frac{4}{1},\frac{1}{0}\right) \end{align*}\]

Le programme suivant permet de calculer les termes successifs de la suite $(u_n)$. Les rationnels sont représentés par des couples d’entiers naturels.

def mediante(r1, r2): return tuple(map(sum, zip(r1, r2))) def sternSuite(n): u = [(0, 1), (1, 0)] l = [] for _ in range(n): v = [mediante(r1, r2) for (r1, r2) in zip(u[1:], u[:-1])] w = [None] * (len(u) + len(v)) w[::2] = u w[1::2] = v u = w l.append(u) return l for u in sternSuite(5): print(u)

Unicité

On peut remarquer que chacune des suites $u_n$ est strictement croissante. Il suffit de raisonner par récurrence sur $n$ en utilisant le résultat du lemme stipulant que la médiante de deux fractions distinctes est strictement comprise entre ces deux fractions. On en déduit en particulier que dans chaque suite $u_n$, chacune des fractions n’apparaît qu’une seule fois.

Irréductibilité

Il est aussi remarquable que toutes les fractions apparaissant dans chaque suite $u_n$ sont irréductibles. Un résultat du lemme permet en effet de montrer par récurrence sur $n$ que si $r=\frac{a}{b}$ et $s=\frac{c}{d}$ sont deux fractions consécutives d’une même suite, alors $\Delta(r,s)=1$ ou encore $bc-ad=1$. En vertu du théorème de Bézout, $(a,b)$ et $(c,d)$ sont des couples d’entiers premiers entre eux, autrement dit les fractions $\frac{a}{b}$ et $\frac{c}{d}$ sont irréductibles.

Existence

Ce qui est plus surprenant est que tout rationnel positif figure à partir d’un certaing rang dans les suites $u_n$. Donnons-nous une fraction $r$ non nulle et non infinie et définissons deux suites $(\rho_n)$ et $(\sigma_n)$ de la manière suivante. On pose $\rho_0=\frac{0}{1}$ et $\sigma_0=\frac{1}{0}$ et tant que $r$ est différent de $\rho_n\oplus\sigma_n$, on pose

\[\left\lbrace \begin{aligned} \rho_{n+1}&=\rho_n\\ \sigma_{n+1}&=\rho_n\oplus\sigma_n \end{aligned} \right. \text{ si } r<\rho_n\oplus\sigma_n \text{ et } \left\lbrace \begin{aligned} \rho_{n+1}&=\rho_n\oplus\sigma_n\\ \sigma_{n+1}&=\sigma_n \end{aligned}\right. \text{ si } \rho_n\oplus\sigma_n<r\]

On vérifie alors que $\rho_n<r<\sigma_n$ tant que $\rho_n$ et $\sigma_n$ sont définis. En particulier, $\Delta(\rho_n,r)>0$ et $\Delta(r,\sigma_n)>0$ et même $\Delta(\rho_n,r)\geq1$ et $\Delta(r,\sigma_n)\geq1$ puisqu’il s’agit d’entiers. On vérifie également que tant que $\rho_n$ et $\sigma_n$ sont définis,

\[S(r)=S(\sigma_n)\Delta(\rho_n,r)+S(\rho_n)\Delta(r,\sigma_n)\geq S(\rho_n)+S(\sigma_n)\]

La suite de terme général $S(\rho_n)+S(\sigma_n)$ est donc une suite d’entiers strictement croissante (le dénominateur et le numérateur des fractions $\sigma_n$ et $\rho_n$ ne peuvent être simultanément nuls) et majorée par $S(r)$ : cette suite est donc finie. Il en est de même des suites $(\rho_n)$ et $(\sigma_n)$, ce qui prouve que $r$ appartient à l’une des suites $u_n$.

Construction de l’arbre de Stern-Brocot

On peut également représenter les fractions apparaissant dans la suite $(u_n)$ sous forme d’un arbre binaire. On place au niveau 0 les fractions $\frac{0}{1}$ et $\frac{1}{0}$ et au niveau 1 la fraction $\frac{1}{1}$ en tant que fils commun de ces deux fractions. On place au niveau $n+1$ de l’arbre par ordre croissant les fractions apparues dans la suite $u_{n+1}$ alors qu’elles ne figuraient pas dans la suite $u_n$ et on donne pour ancêtre de chacune de ces fractions la fraction du niveau $n$ dont on s’est servi pour la calculer en tant que médiante. L’arbre ainsi construit est appelé arbre de Stern-Brocot.

Voici par exemple l’arbre de Stern-Brocot construit jusqu’au niveau 6.2

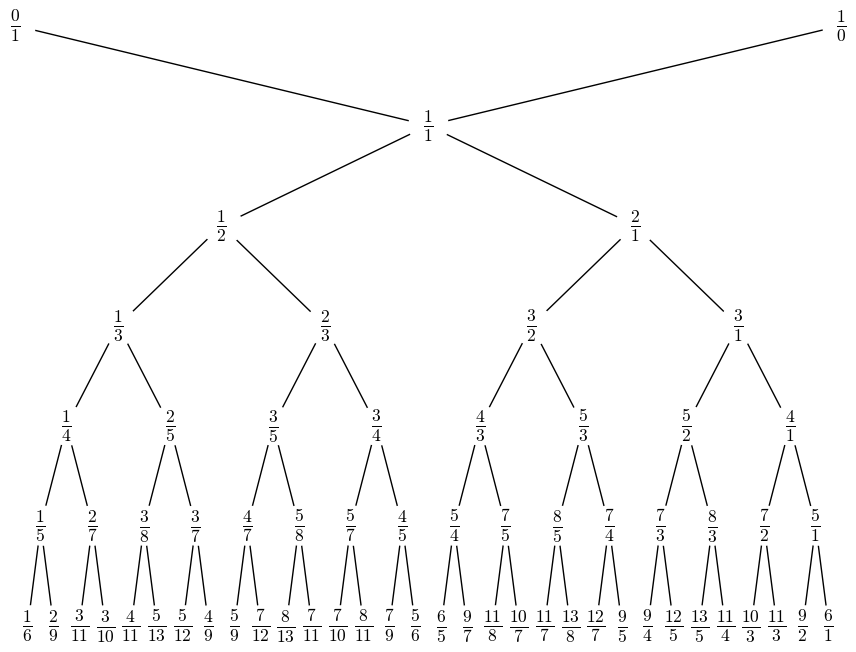
Arbre de Stern-Brocot

Par exemple, la fraction $\frac{3}{5}$ apparaît au niveau 4 et a été calculée comme médiante des fractions $\frac{1}{2}$ et $\frac{2}{3}$. Comme $\frac{2}{3}$ est apparue au niveau 3 tandis que $\frac{1}{2}$ est apparue au niveau 2, on décrète que $\frac{3}{5}$ est le fils de $\frac{2}{3}$.

Chaque rationel de $\mathbb Q_+$ apparaît une et une seule fois dans l’arbre. On peut donc construire une suite prenant une et une seule fois chaque valeur dans $\mathbb Q_+$ : il suffit pour cela de numéroter les noeuds de l’arbre de Stern-Brocot (en laissant de côté la fraction $\frac{1}{0}$), par exemple de haut en bas puis de gauche à droite. Cette suite réalise donc une bijection de $\mathbb N$ sur $\mathbb Q_+$. Autrement dit, $\mathbb Q_+$ est dénombrable.

Calcul des descendants

Il est alors facile de déterminer les fils gauche et droit d’un noeud de l’arbre connaissant ses ancêtres. Pour déterminer le fils gauche, on calcule la médiante du noeud considéré et de son premier ancêtre qui lui est inférieur tandis que pour déterminer le fils droit, on calcule la médiante du noeud considéré et du premier ancêtre qui lui est supérieur. Par exemple, le premier ancêtre de $\frac{5}{8}$ qui lui est inférieur est $\frac{3}{5}$ et son premier ancêtre qui lui est supérieur est $\frac{2}{3}$ donc les fils gauche et droit de $\frac{5}{8}$ sont respectivement $\frac{5}{8}\oplus\frac{3}{5}=\frac{8}{13}$ et $\frac{5}{8}\oplus\frac{2}{3}=\frac{7}{11}$. De même, les fils gauche et droit de $\frac{5}{4}$ sont $\frac{5}{4}\oplus\frac{1}{1}=\frac{6}{5}$ et $\frac{5}{4}\oplus\frac{4}{3}=\frac{9}{7}$.

Calcul des ancêtres

L’algorithme utilisé dans la section Existence permet également de retrouver les ancêtres d’une fraction donnée dans l’arbre de Stern-Brocot. Il nous donne en effet la liste des médiantes utilisées pour aboutir à cette fraction.

def mediante(r1, r2): return tuple(map(sum, zip(r1, r2))) def delta(r1, r2): return r2[0] * r1[1] - r1[0] * r2[1] def sternAncetres(x): a, b, c = (0, 1), (1, 0), (1, 1) l = [c] while delta(c,x)!=0: if delta(c, x) > 0: a = c else: b = c c = mediante(a, b) l.append(c) return l print(sternAncetres((13, 55)))

Un peu d’arithmétique

Soit $r=\frac{p}{q}$ une fraction non nulle et non infinie. On sait que cette fraction est la médiante de deux fractions $\rho=\frac{a}{b}$ et $\sigma=\frac{c}{d}$ telles que $\Delta(\rho,\sigma)=1$. Cette dernière égalité montrer que $b\geq1$ et $c\geq1$. Par ailleurs, $p=a+c$ et $q=b+d$ donc $0\leq a\leq p-1$ et $0\leq d\leq q-1$. Enfin,

\[\begin{align*} bp-aq&=\Delta(\rho,r)=\Delta(\rho,\rho\oplus\sigma)=\Delta(\rho,\sigma)=1\\ cq-dp&=\Delta(r,\sigma)=\Delta(\rho\oplus\sigma,\sigma)=\Delta(\rho,\sigma)=1 \end{align*}\]

de sorte que $bp\equiv1[q]$ et $cq\equiv1[p]$. Ainsi $b$ est l’inverse de $p$ modulo $q$ et $c$ est l’inverse de $q$ modulo $p$3 (les inverses sont bien définis car $p$ et $q$ sont premiers entre eux). Les conditions $bp-aq=1$ et $cq-dp=1$ définissent alors également $a$ et $d$.

Les deux fractions $\rho$ et $\sigma$ sont des ancêtres de $r$ dans l’arbre de Stern-Brocot et l’une d’elles est son père. On remarque alors que la fonction $S$ croît strictement le long d’un chemin de l’arbre : le père de $r$ est donc la fraction dont l’image par $S$ est la plus grande. On en déduit un algorithme de calcul du père d’une fraction dans l’arbre de Stern-Brocot. Les inverses modulaires sont calculés à l’aide d’un algorithme d’Euclide étendu.

def sternEncadre(x): p, q = x r, u, v, rr, uu, vv = p, 1, 0, q, 0, 1 while rr != 0: k = r // rr r, u, v, rr, uu, vv = rr, uu, vv, r - k * rr, u - k * uu, v - k * vv p, q = p // r, q // r a, d = -v % p, -u % q b, c = (1 + a * q) // p, (1 + d * p) // q return (a, b), (c, d) def sternPere(x): r1, r2 = sternEncadre(x) return r1 if sum(r1) > sum(r2) else r2 print(sternPere((17,38)))

On peut également voir l’algorithme décrit dans la section Existence comme un algorithme d’Euclide étendu. En utilisant les mêmes notations que dans cet algorithme, on montre que $\Delta(\rho_n,\sigma_n)=1$ est un invariant de boucle. A la dernière étape, $r=\rho_N\oplus\sigma_N$ pour un certain entier $N$ donc

\[\Delta(\rho_N,r)=\Delta(r,\sigma_N)=\Delta(\rho_N,\sigma_N)=1\]

  1. Petit exercice facile : calculer le nombre de termes de $u_n$ en fonction de $n$. ↩

  2. Petit exercice facile à nouveau : montrer que le plus grand numérateur ou dénominateur des fractions du niveau $n$ est le terme de rang $n+1$ de la suite de Fibonacci. ↩

  3. Si $x$ et $n$ sont deux entiers naturels premiers entre eux, $n$ étant non nul, on appelle inverse de $x$ modulo $n$ l’unique entier $y$ tel que $0\leq y\leq n-1$ et $xy\equiv1[n]$. ↩