Suite logistique

Introduction

La suite logistique est un système dynamique discret permettant de modéliser l’évolution d’une population. Plus précisément, on considère la suite $(u_{n})$ vérifiant la relation de récurrence suivante :

\forall n \in N, u_{n + 1} = r \cdot u_{n} \cdot (1 - u_{n})

Le terme $u_{n}$ ne représente pas à proprement parler la population mais une fraction d’une population maximale donnée. Pour que la suite $(u_{n})$ reste à valeurs dans $[0, 1]$ , on s’aperçoit qu’il faut choisir $r$ dans $[0, 4]$ .

Simulation

L’animation GeoGebra suivante représente les termes de cette suite.

Il est en particulier intéressant de prendre l’indice $k$ du premier terme représenté de l’ordre de $50$ pour avoir une idée du comportement asymptotique de cette suite. Pour plus de précision, on peut faire varier le paramètre $r$ à l’aide des flèches directionnelles : il se passe des choses intéressantes pour $r \in [3, 4]$ .

Comportement asymptotique

Si $u_{0} \in {0, 1}$ , il est clair que la suite $(u_{n})$ est nulle à partir du rang $1$ quelle que soit la valeur de $r$ . On suppose donc $u_{0} \in] 0, 1 [$ dans la suite.

Lorsque $r \in [0, 1]$ , on voit clairement que $(u_{n})$ converge vers $0$ .
Lorsque $r \in] 1, 3]$ , la suite $(u_{n})$ converge vers un point fixe non nul de $f$ (elle est mononotone à partir d’un certain rang si $r \in] 1, 2]$ tandis que les suites $(u_{2 n})$ et $(u_{2 n + 1})$ sont adjacentes à partir d’un certain rang lorsque $r \in] 2, 3]$ ).
Lorsque $r \in] 3, 4]$ , les choses se compliquent. La suite $(u_{n})$ admet d’abord un cycle-limite¹ de longueur $2$ , puis de longueur $4$ , $8$ , $16$ … Tous les cycles de longueur une puissance de $2$ apparaissent jusqu’à une certaine valeur de $r$ à partir de laquelle commence le chaos : l’évolution asymptotique de la suite $(u_{n})$ est “imprévisible”² et dépend grandement de la condition initiale. Néanmoins, il existe certains intervalles isolés de valeurs de $r$ pour lesquelles la suite $(u_{n})$ converge à nouveau vers un cycle-limite. On peut montrer que l’apparition des longueurs des cycles-limites suit un certain ordre appelé ordre de Charkovski.

Diagramme de Feigenbaum

Pour mieux comprendre ce qui précède, on trace les valeurs d’adhérences³ de la suite $(u_{n})$ en fonction des valeurs de $r$ .

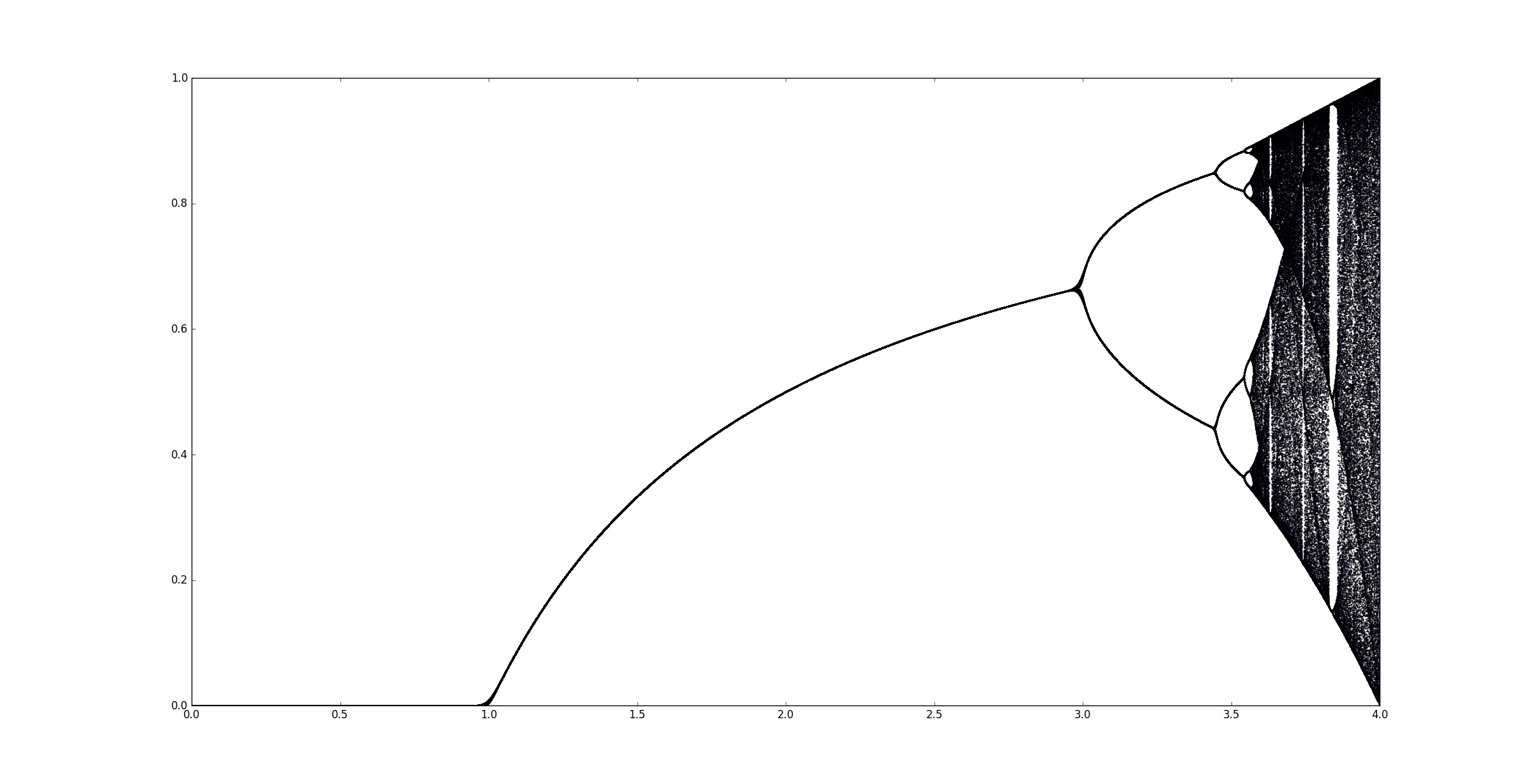
Diagramme de Feigenbaum

Les résultats sont cohérents avec ce qui a été décrit précédemment. On observe notamment le doublement de la longeur du cycle limite à partir de $r = 3$ .

On peut zoomer pour voir plus précisément ce qui se passe pour $r \in [3, 4]$ .

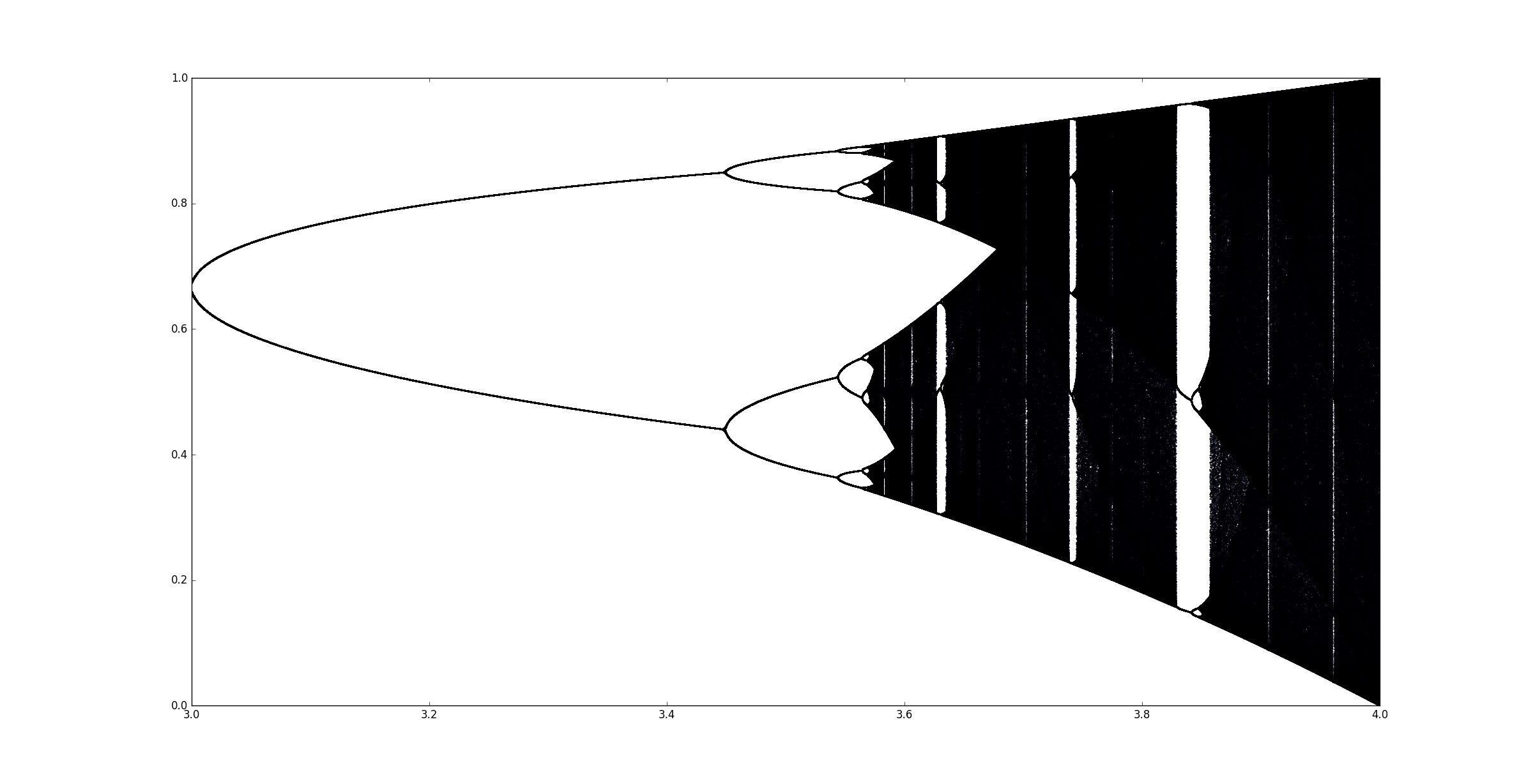
Diagramme de Feigenbaum

On peut aussi remarquer en zoomant qu’on obtient également des cycles de longeur qui ne sont pas des puissances de $2$ .

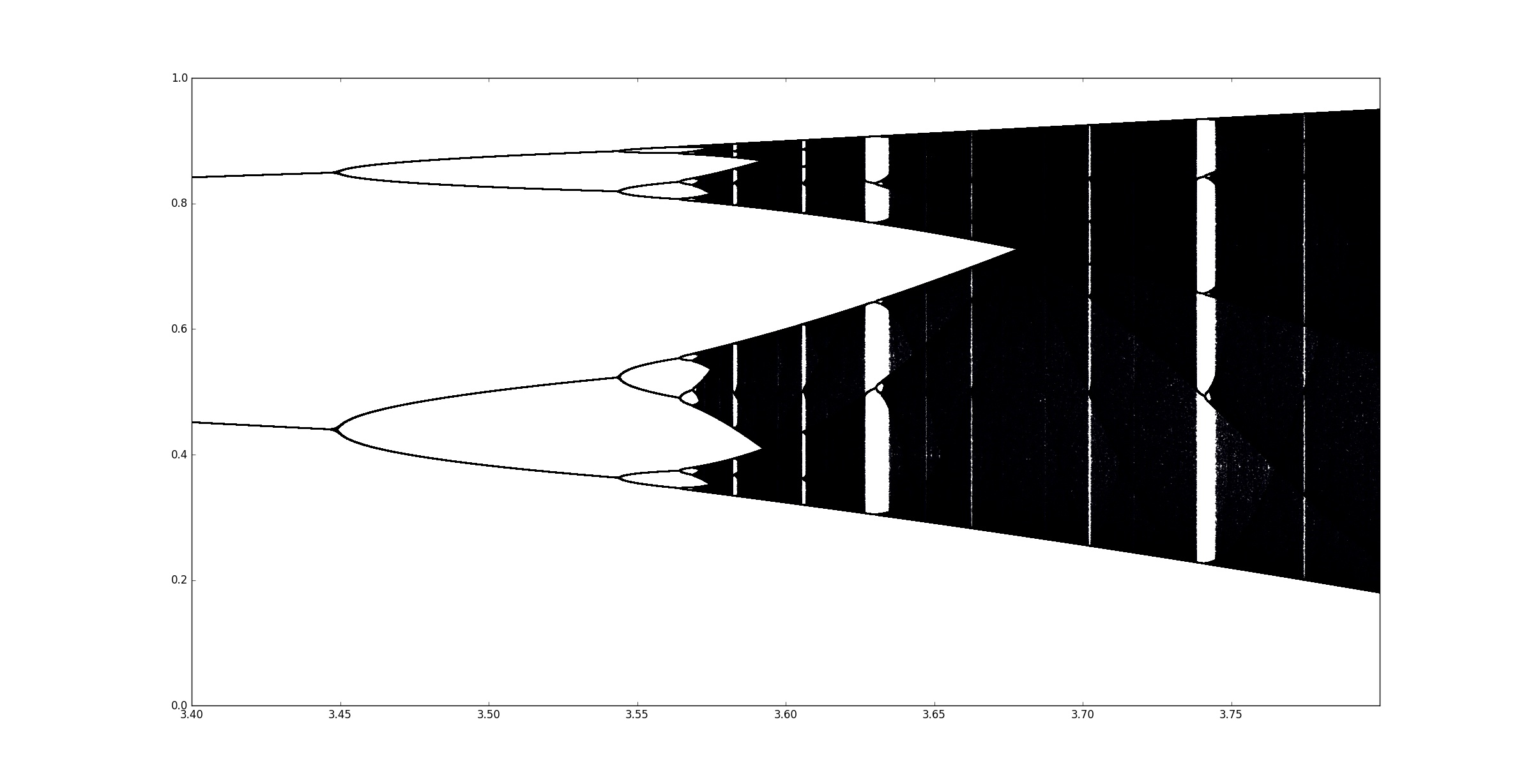
Diagramme de Feigenbaum

Le principe de doublement de la longueur du cycle reste encore valable. Dans la figure suivante, on voit apparaître successivement des cycles de longeur⁴ $3$ , $6$ , $12$ …

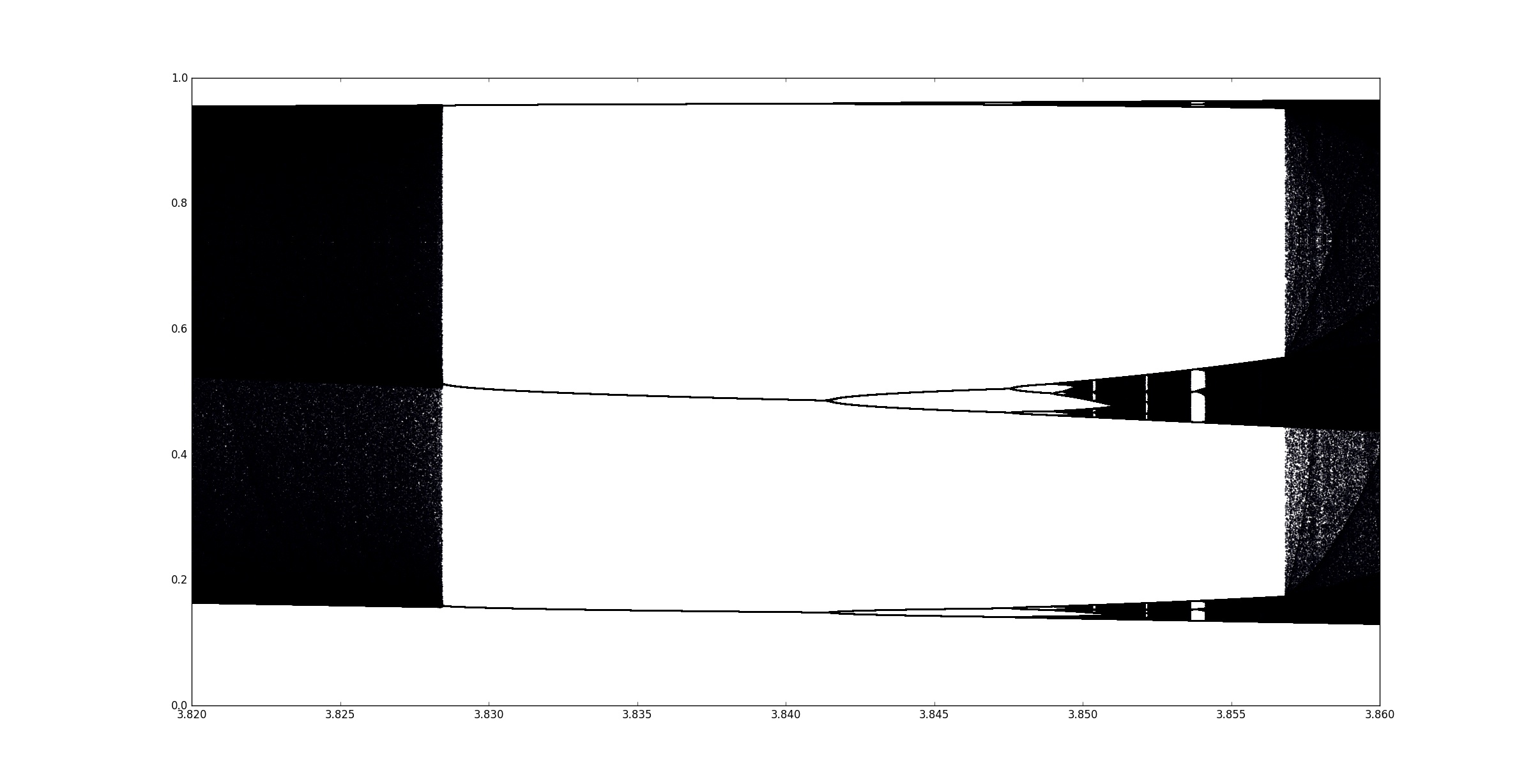
Diagramme de Feigenbaum

Code Python

Voilà la fonction Python utilisée pour le tracé du diagramme de Feigenbaum.

from numpy import linspace
from matplotlib.pyplot import scatter, show, xlim, ylim

def f(r, x):
    return r * x * (1 - x)

def feigenbaum(r1, r2, nb, N):
    r_range = linspace(r1, r2, nb)
    x = []
    y = []
    for r in r_range:
        u = .1
        for _ in range(N):
            u = f(r, u)
        for _ in range(N):
            u = f(r, u)
            x.append(r)
            y.append(u)
    scatter(x, y, marker='.', s=1)
    xlim(r1, r2)
    ylim(0, 1)
    show()

On dira qu’une suite $(u_{n})$ admet un cycle-limite de longueur $p$ si les suites extraites $(u_{n + k})$ pour $0 \leq k \leq p - 1$ convergent. ↩
Bien entendu, les valeurs des termes de la suite sont encore calculables par récurrence donc l’évolution de la suite est encore “prévisible”. Mais il n’existe plus de comportement asymptotique aussi régulier qu’un cycle-limite. ↩
On appelle valeur d’adhérence d’une suite toute limite éventuelle d’une de ses suites extraites. ↩
Je concède qu’il faille faire preuve d’imagination… ↩