Champ de vecteurs

On appelle champ de vecteurs une application de $R^{n}$ dans $R^{n}$ . Les éléments de l’ensemble de départ sont vus comme des points tandis que les éléments de l’ensembles d’arrivée sont vus comme des vecteurs.

Par exemple, en physique, les champs électrique et magnétiques sont des champs de vecteur : à tout point de l’espace sont associés deux vecteurs $\vec{E}$ et $\vec{B}$ .

En dimension $2$ ou $3$ , on peut visualiser un champ de vecteurs $f$ en dessinant le vecteur $f (X)$ en tout point $X$ .

Voici par exemple ce que donne la représentation du champ de vecteurs $f : (x, y) \in R^{2} \mapsto (- y, x)$

Champ de vecteurs

Maintenant une représentation d’un champ de vecteur un peu plus complexe $f : (x, y) \in R^{2} \mapsto (\sin (x \cdot y / 10), \cos (x \cdot y / 10))$

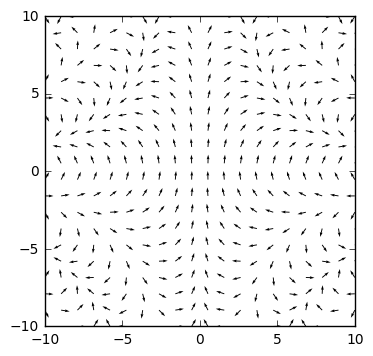
Champ de vecteurs

from math import sin, cos
from numpy import linspace, meshgrid, vectorize
from matplotlib.pyplot import quiver, show, axis, gca

def f(x,y):
    return sin(.1*x*y), cos(.1*x*y)
x, y = meshgrid(linspace(-10, 10, 20), linspace(-10, 10, 20))
dx, dy = vectorize(f)(x, y)
gca().set_aspect('equal', adjustable='box')
quiver(x, y, dx, dy)
show()

Application aux systèmes différentiels

De manière générale, un système différentiel autonome peut s’écrire sous la forme $X^{'} = f (X)$ où

$X = (x_{1}, \dots, x_{n})$ est une application inconnue de classe $C^{1}$ sur $R$ à valeurs dans $R^{n}$ ;
$f$ est une application continue de $R^{n}$ dans $R^{n}$ , c’est-à-dire un champ de vecteurs.

Voici par exemple le système différentiel en dimension 2 associé au champ de vecteurs $f : (x, y) \mapsto (- y, x)$ :

{\begin{aligned} x^{'} & = - y \\ y^{'} & = x \end{aligned}

Dans le cas où $f$ est un endomorphisme de $R^{n}$ , on parle de système différentiel linéaire. On sait alors résoudre explicitement un tel système. Dans le cas où $f$ n’est pas linéaire, le thèorème de Cauchy-Lipschitz garantit l’existence d’une solution et son unicité si l’on fournit des conditions initiales (à condition que $f$ soit suffisamment régulier) mais ce n’est pas notre propos. On préfère ici expliquer comment prévoir l’évolution d’une solution d’un système linéaire à partir de la représentation graphique du champ de vecteurs.

Une application $X$ solution du système peut être vue comme une courbe paramétrée à valeurs dans $R^{n}$ . A chaque instant $t$ , le vecteur vitesse $X^{'} (t)$ est égal à $f (X (t))$ , c’est-à-dire que la trajectoire de $X$ est “guidée” par le champ de vecteurs.

Voilà par exemple l’évolution d’une solution du sytème différentiel

{\begin{aligned} x^{'} & = - y \\ y^{'} & = x \end{aligned}

Le premier graphique représente l’évolution de $x$ et $y$ en fonction du temps.
Le second graphique représente l’évolution de la courbe paramétrée $(x, y)$ superposée à la représentation graphique du champ de vecteurs.

Même chose pour le système différentiel :

{\begin{aligned} x^{'} & = x / 5 + 5 y \\ y^{'} & = - 5 x + y / 5 \end{aligned}

Enfin, un exemple de système différentiel non linéaire sans doute un peu plus probant :

{\begin{aligned} x^{'} & = \exp (\cos (x) / 2) \cdot \sin (y^{2} / 20) \\ y^{'} & = 2 \cos (x^{2} / 5) \end{aligned}

from scipy.integrate import odeint
from numpy import array, linspace, meshgrid, cos, sin, exp
from matplotlib.pyplot import figure, plot, grid, legend, xlabel, ylabel, show, xlim, ylim, subplot, gca, quiver
from matplotlib.animation import FuncAnimation
from numpy import vectorize


def f(x1, x2):
    return exp(cos(x1) / 2) * sin(x2 ** 2 / 20), 2 * cos(x1 ** 2 / 5)


def diff(X, t=0):
    return [*f(X[0], X[1])]


t = linspace(0, 30, 2000)
X0 = array([1, 0])

X = odeint(diff, X0, t)
x1_sol, x2_sol = X.T

x1_min, x1_max, x2_min, x2_max = min(x1_sol), max(x1_sol), min(x2_sol), max(x2_sol)
x1_range, x2_range = x1_max - x1_min, x2_max - x2_min
x1_min, x1_max, x2_min, x2_max = x1_min - .1 * x1_range, x1_max + .1 * x1_range, x2_min - .1 * x2_range, x2_max + .1 * x2_range
x, y = meshgrid(linspace(x1_min, x1_max, 20), linspace(x2_min, x2_max, 20))
dx, dy = vectorize(f)(x, y)

fig = figure(figsize=(10, 5))

subplot(121)
grid()
xlim([min(t), max(t)])
ylim([min(x1_min, x2_min), max(x1_max, x2_max)])
p1, = plot([], [], 'r-', label="$x$")
p2, = plot([], [], 'b-', label="$y$")
legend()

subplot(122)
grid()
gca().set_aspect('equal', adjustable='box')
xlim([x1_min, x1_max])
ylim([x2_min, x2_max])
xlabel("$x$")
ylabel("$y$")
p3, = plot([], [], 'g-')
p4, = plot([], [], 'go')
quiver(x, y, dx, dy)


def animate(i):
    p1.set_data(t[:i], x1_sol[:i])
    p2.set_data(t[:i], x2_sol[:i])
    p3.set_data(x1_sol[:i], x2_sol[:i])
    p4.set_data(x1_sol[i], x2_sol[i])
    return p1, p2, p3, p4


ani = FuncAnimation(fig, animate, range(len(t)), interval=10, blit=True)

show()

De manière imagée, la trajectoire d’une solution d’un système différentiel correspond à la trajectoire d’un bouchon de liège sur une eau agitée par des courants. Le champ de vitesses dans un fluide n’est d’ailleurs qu’un exemple de champ de vecteurs…