Récemment, j’ai vu une belle vidéo sur Youtube où il était question de figures obtenues à l’aide de tables de multiplication. Plus précisément,

• on fixe un entier $r$ ;
• on dispose régulièrement des points sur le cercles unité numérotés de $0$ à $n-1$ ;
• on relie chaque point $k$ au point dont le numéro est le reste de la division euclidienne de $rk$ par $n$.

Par exemple, lorsque $n=10$ et $r=2$, on obtient la figure suivante.

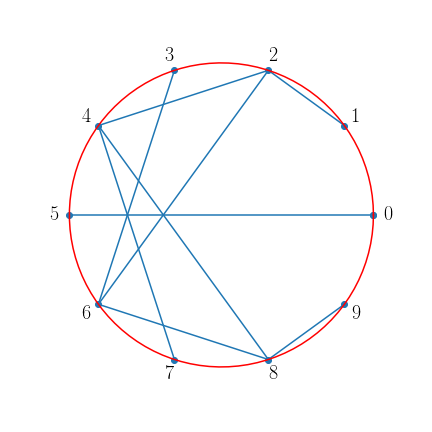
En fait, le point numéroté $k$ a pour coordonnées $(\cos(k\pi/n),\sin(k\pi/n))$ et on le relie au point de coordonnées $(\cos(rk\pi/n),\sin(rk\pi/n))$. Ceci a l’avantage de pouvoir généraliser le procédé décrit plus haut à des tables de multiplications de $r$ même si $r$ n’est pas entier.

Lorsque l’on prend un grand nombre $n$ de points et que l’on fait varier continûment $r$, on obtient des animations du style suivant.

Bien évidemment, je me pose deux questions :

• comment obtenir ces animations ?
• pourquoi obtient-on de telles figures ?

Un peu de Python

On peut obtenir les animations précédentes à l’aide du langage Python.

On commence par les import nécessaires au chargement des bibliothèques classiques.

import matplotlib.animation as ani
import matplotlib.collections as mc
import matplotlib.pyplot as plt
import numpy as np

On définit une fonction permettant de récupérer la liste des segments de droites à tracer. Chaque segment est une liste des coordonnées des extrémités du segment.

def get_lines(t, r):
    x1 = np.cos(t)
    y1 = np.sin(t)
    x2 = np.cos(r * t)
    y2 = np.sin(r * t)
    lines = [[(x1, y1), (x2, y2)] for x1, y1, x2, y2 in zip(x1, y1, x2, y2)]
    return lines

Enfin, on crée l’animation à proprement parler. On utilise pour cela la sous-bibliothèque de matplotlib dédiée à l’animation.

fig=plt.figure(figsize=(6, 6))
t = np.linspace(0, 2 * np.pi, 300)
plt.axis('equal')
plt.axis('off')
lc = mc.LineCollection([])
ax=plt.gca()
ax.add_collection(lc)
ax.autoscale()


def animate(frame):
    lc.set_paths(get_lines(t, frame))
    lc.set_linewidth(.2)
    ax.set_xlim(-1.1, 1.1)
    ax.set_ylim(-1.1, 1.1)
    return lc,


anim = ani.FuncAnimation(fig, animate, frames=np.linspace(
    0, 10, 1000), interval=10, blit=True)
plt.show()

Essentiellement, la fonction animate met à jour la liste des segments à tracer. Le paramètre frame n’est autre que le facteur de multiplication $r$.

Et c’est tout.

Pourquoi de si belles figures ?

C’est un problème classique de géométrie différentielle : une famille de courbes (par exemple de droites) “forme” une nouvelle courbe. La courbe ainsi formée est appelée l’enveloppe de cette famille de courbes.

Par exemple, dans la figure suivante, l’enveloppe de la famille de droites est un cercle.

Pour être plus rigoureux, l’enveloppe d’une famille de droites (ou plus généralement de courbes) est une courbe tangente à chacune de celles-ci. Dans notre cas, on cherche donc une courbe tangente à tous les droites passant par les points de coordonnées $(\cos(\te),\sin(\te))$ et $(\cos(r\te),\sin(r\te))$ lorsque $\te$ décrit $\dR$.

On va dans un premier temps définir quelques notations. On note

• $\cC$ la courbe enveloppe recherchée ;
• $\mathbf{u}(\te)=(\cos\te,\sin\te)$ et $\mathbf{v}(\te)=(-\sin\te,\cos\te)$ ;
• $\cD(\te)$ la droite passant par les points de coordonnées $\mathbf{u}(\te)$ et $\mathbf{v}(\te)$ ;
• $\mathbf{m}(\te)$ les coordonnées du point en lequel la courbe $\cC$ est tangente à la droite $\cD(\te)$.

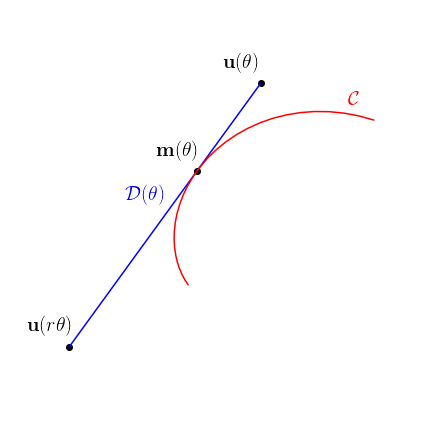
On remarque en particulier que $\mathbf{u}’=\mathbf{v}$.

Puisque le point de coordonnées $\mathbf{m}(\te)$ est sur la droite $\cD(\te)$, il existe un réel $\la(\te)$ tel que

On va supposer la fonction $\la$ dérivable sur $\dR$. Puisque la droite $\cD(\te)$ est tangente à $\cC$, le vecteur de coordonnées $\mathbf{m}’(\te)$ est un vecteur directeur de la droite $\cD(\te)$ de sorte que

On obtient aisément

Le déterminant étant bilinéaire et alterné, on en déduit

A nouveau, en utilisant la bilinéarité du déterminant,

On en déduit donc que lorsque $\cos((r-1)\te)\neq0$,

Comme on a supposé $\la$ dérivable et a fortiori continue, cette égalité est en fait toujours valable.

Finalement,

Réciproquement, on vérifie aisément qu’une telle courbe paramétrée vérifie la condition de tangence requise.

En prenant un faible nombre de segments, on peut visualiser la tangence de ces segments à la courbe ($r=2$ dans la figure suivante).

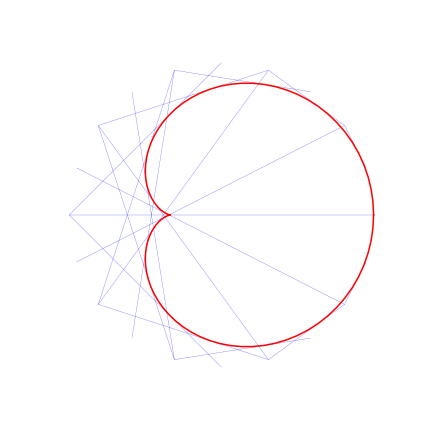
On peut enfin superposer l’enveloppe ainsi déterminée à l’animation précédente.