Tout le code intervenant dans cet article est disponible dans ce notebook Jupyter.
from random import random
from math import floor, log, exp, factorial
Python dipose d’un module random dans la bibliothèque standard. La fonction du même nom de ce module renvoie un nombre aléatoire suivant une loi uniforme sur $[0,1[$. La variable aléatoire $U$ associée n’est pas une variable aléatoire discrète puisque son support $[0,1[$ n’est pas dénombrable. On sort donc du cadre du programme de classes préparatoires en probabilités. Néanmoins, il suffit de comprendre pour la suite que cette variable aléatoire vérifie la propriété suivante
Loi de Bernoulli
Il est alors très simple de simuler une variable aléatoire suivant une loi de Bernoulli de paramètre $p\in[0,1]$. En effet, en posant $X=\un_{\lbrace U<p\rbrace}$, on a
\[\begin{aligned} \dP(X=1)&=\dP(U<p)=\dP(U\in[0,p[)=p-0=p\\ \dP(X=0)&=\dP(U\geq p)=\dP(U\in[p,1[)=1-p \end{aligned}\]On peut alors définir une fonction bernoulli simulant une variable aléatoire de Bernoulli de paramètre $p$.
def bernoulli(p):
return 1 if random() < p else 0
Loi binomiale
Comme on sait que la somme de $n$ variables aléatoires indépendantes suivant la même loi de Bernoulli de paramètre $p$ suit la loi binomiale de paramètres $n$ et $p$, il n’est alors pas difficile d’écrire une fonction simulant une variable aléatoire suivant cette loi.
def binomial(n, p):
return sum(bernoulli(p) for _ in range(n))
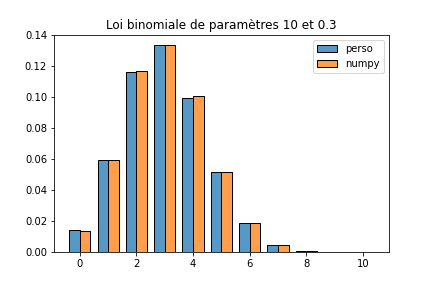
Pour vérifier que cette fonction a bien le comportement escompté, on peut comparer l’histogramme des fréquences obtenues avec notre fonction lors d’un grand nombre de simulations avec celui obtenu via la fonction binomial du module numpy.random.
Loi uniforme
Si l’on souhaite simuler une loi uniforme sur $\lbrace0,1,\dots,n-1\rbrace$, on pose $X=\lfloor nU\rfloor$. Ainsi
\[\begin{aligned} \forall k\in\lbrace0,1,\dots,n-1\rbrace,\;\dP(X=k)&=\dP(\lfloor nU\rfloor=k)\\ &=\dP(nU\in[k,k+1[)\\ &=\dP\left(U\in\left[\frac{k}{n},\frac{k+1}{n}\right[\right)\\ &=\frac{k+1}{n}-\frac{k}{n}=\frac{1}{n} \end{aligned}\]def uniform(n):
return floor(n*random())
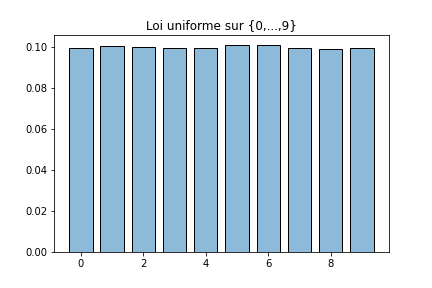
A nouveau, on vérifie bien expérimentalement à l’aide d’un grand nombre de simulations que cette fonction simule bien une loi uniforme.
Si l’on souhaite simuler une loi uniforme sur un ensemble fini $E=\lbrace e_0,\dots,e_{n-1}\rbrace$, il suffit de modéliser cet ensemble par une liste $\mathtt{[e_0,\dots,e_{n-1}]}$.
def uniform(n):
if type(n) == int:
return floor(n*random())
if type(n) == list:
return n[uniform(len(n))]
Loi géométrique
On sait la loi géométrique est la loi du temps d’attente du premier succès lors de la répétition d’épreuves de Bernoulli mutuellement indépendantes. On peut donc simuler cette loi à l’aide de la fonction bernoulli précédement définie de la manière suivante.
def geometric(p):
n = 1
while bernoulli(p) == 0:
n += 1
return n
Néanmoins ceci peut se révéler inefficace surtout pour de faibles valeurs de $p$ puisque le nombre d’itérations de la boucle while n’est pas majoré.
Remarquons que si $X$ suit la loi géométrique de paramètre $n$, alors en notant classiquement $q=1-p$ :
\[\forall n\in\dN,\;\dP(X\leq n)=\sum_{k=1}^nq^{k-1}p=p\cdot\frac{1-q^n}{1-q}=1-q^n\]def geometric(p):
return floor(log(1-random())/log(1-p))+1
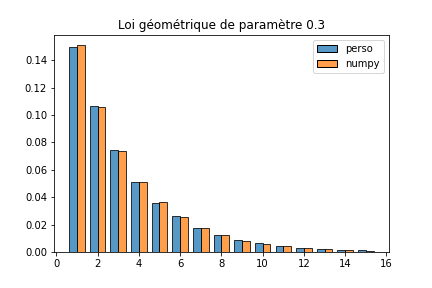
A nouveau, on peut comparer l’histogramme des fréquences obtenues avec notre fonction avec celui obtenu avec la fonction geometric du module numpy.random.
Loi à support fini
On souhaite simuler une variable aléatoire $X$ de loi suivante :
\[\forall k\in\lbrace0,\dots,n-1\rbrace,\;\dP(X=k)=p_k\]Proposition. Soit $(p_0,\dots,p_{n-1})$ une famille de termes positifs et de somme $1$. On note
\[\forall k\in\lbrace0,\dots,n-1\rbrace,\;S_k=\sum_{j=0}^kp_k\]et on convient que $S_{-1}=0$. Alors si $U$ suit une loi uniforme sur $[0,1[$ et si
\[X=\inf\left\lbrace k\in\lbrace0,\dots,n-1\rbrace,\;U<S_n\right\rbrace\]alors $\dP(X=k)=p_n$ pour tout $k\in\lbrace0,\dots,n-1\rbrace$.
Preuve. Il suffit de remarquer que
\[\begin{aligned} \forall k\in\lbrace0,\dots,n-1\rbrace,\;\dP(X=k)&=\dP(S_{k-1}\leq U<S_k)\\ &=\dP(U\in[S_{k-1},S_k[)\\ &=S_k-S_{k-1}=p_k \end{aligned}\]On en déduit l’algorithme suivant où proba désigne une liste de réels positifs de somme 1.
def fini(proba):
r = random()
s = sum(proba)
sp = proba[0]
n = 0
while r >= sp:
n += 1
sp += proba[n]
return n
Mais si jamais l’utilisateur ne fournit pas une liste de réels de somme 1, on peut normaliser les éléments de cette liste.
def fini(proba):
r = random()
s = sum(proba)
sp = proba[0]/s
n = 0
while r >= sp:
n += 1
sp += proba[n]/s
return n
On vérifie encore une fois expérimentalement la correction de cette fonction.
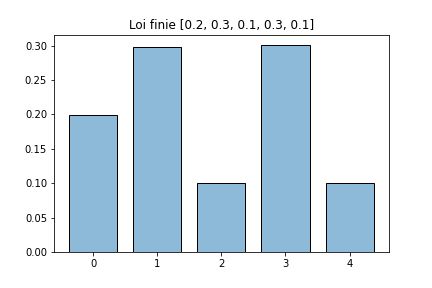
Loi à support dénombrable
On souhaite simuler une variable aléatoire $X$ de loi suivante :
\[\forall k\in\dN,\;\dP(X=n)=p_n\]Proposition. Soit $\sum_{n\in\dN}p_n$ une série à termes positifs et de somme $1$. On note
\[\forall n\in\dN,\;S_n=\sum_{k=0}^np_k\]sa somme partielle de rang $n$ et on convient que $S_{-1}=0$. Alors si $U$ suit une loi uniforme sur $[0,1[$ et si
\[X=\inf\lbrace n\in\dN,\;U<S_n\rbrace\]alors $\dP(X=n)=p_n$ pour tout $n\in\dN$.
Preuve. Il suffit de remarquer que
\[\forall n\in\dN,\;\dP(X=n)=\dP(S_{n-1}\leq U<S_n)=\dP(U\in[S_{n-1},S_n[)=S_n-S_{n-1}=p_n\]On en déduit l’algorithme suivant où proba désigne une fonction prenant en argument un entier naturel $n$ et renvoyant un réel $p_n$ tel que $\sum_{n\in\dN}p_n$ soit une série de terme positifs et de somme 1.
def infini(proba):
r = random()
n = 0
s = proba(0)
while r >= s:
n += 1
s += proba(n)
return n
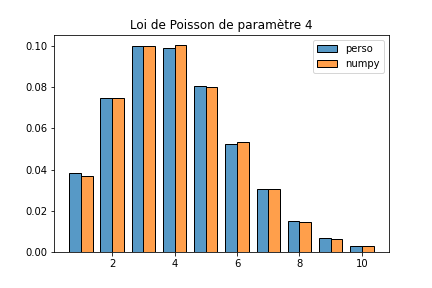
Par exemple, si la fonction poisson suivante simule une variable aléatoire de paramètre l donné.
poisson=lambda l: infini(lambda n: exp(-l)*l**n/factorial(n))